ABC 214G : Three Permutations
問題文:https://atcoder.jp/contests/abc214/tasks/abc214_g
問題概要
日本語なので略。
公式解説を読んでて分からなかったところだったり、自分が類題を解くときにつまづきそうなところだったりをメモがてら書きます。
解法
パート1. 包除原理
の順列全体の集合を
と書くことにする。この問題の条件を満たす順列全体の集合を
とすると
ここで、 に対して、集合
を
と置くと、 が成立する。
余事象を取ると
が成り立つ。
ここで、 とおき、要素数に注目すると
が成り立つ。 の項に対して包除原理を適用することで
ここで、 を固定したとき、
について考察する。
を一つとると、
を満たす
同士で自由に
の値を入れ替えた順列
も
の元となる。したがって、
は
の倍数である。
つまるところ、 としたとき、
が成立する。*1
したがって、 と置くことで、
と書ける。よって
に対して
が求められればこの問題を解くことができる。
パート2. 各 に対して
を求める
これは解説に述べられている通りである。からなるグラフ
を考える。すべての頂点の次数が
なので、
はサイクルと自己ループからなるグラフである。
ここで、グラフを、辺集合が
、頂点集合が
の端点全体の集合
となるグラフと定義する。
はサイクル、自己ループ、およびパスからなるグラフである。
この記号のもと、は
の各辺に対して隣接している頂点を割り当てる組み合わせの総数となることに注意する。このとき、任意の
に対して、以下のように
が計算できる。
が自己ループのとき、明らかに
。
がサイクルのとき、サイクルに属する辺のうち 1 本にどの頂点を割り当てるかを決めると自動的に残りの辺の割り当ても決まるため
。
がパスのとき、どの辺にも割り当てない頂点を 1 つ決めると、すべての辺に対して頂点の割り当てが一意になる。したがって、パスに属する頂点数を
とすると
。
が複数の連結成分から構成される場合、
はそれぞれの連結成分ごとに上記の通り数の積を求めたもの。
パート3. 複数の をまとめて求める
パート 2. で求めたをすべての部分集合について愚直に計算すると
時間かかってしまう。そこで、ひとつの連結成分に含まれる部分グラフ
すべてについて
を効率的に求めることを考える。それぞれの連結成分ごとに
の和を
の大きさごとに格納したテーブルを用意できれば、それらのマージは合計
時間でできる。*2
この問題では、部分グラフとしてはサイクルとパスのみを考えれば良い。
パスグラフ
の部分グラフ
のうち、辺集合のサイズが
のものについての
の和 (
)
サイクルグラフ
の部分グラフ
のうち、辺集合のサイズが
のものについての
の和 (
)
とする。
まず、 は、以下のグラフから
本の辺を抜いたグラフ(孤立点は無視する)を考えることで、
と書けることがわかる。*3。

と置き直すことで、
と書ける。
ここで、
と定義すると、 である。また、
となることにも留意する。
まず、 の値で場合分けすることにより、
となることがわかる。
また、と書けるため、
という累積和テーブルを
テーブルと一緒に計算することで、
は
の昇順で計算することで各要素あたり
時間で計算できる。これで
は効率的に計算することができる。
については、
であることはパート 2. で確認済みである。
のとき、
はいくつかのパスから成るグラフである。
の各辺に下図のように番号を振って、取り除かれた辺のうち最小のものに対する
の定義式の
の値で場合分けをすることにより、
と書けることがわかる。
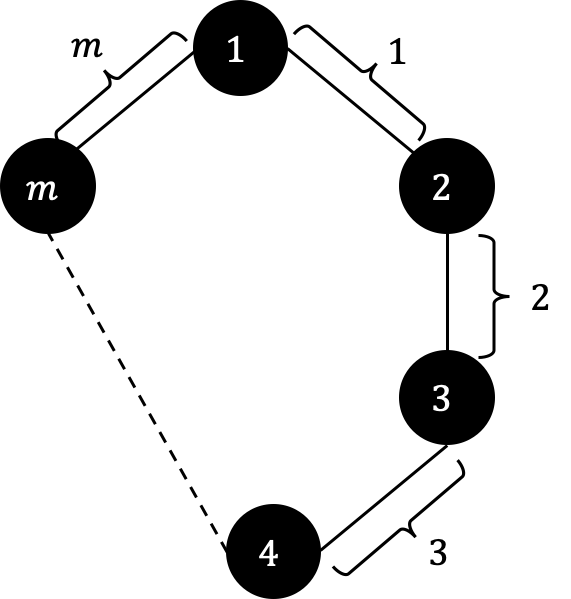
したがって全体で でこの問題を解くことができた。
感想
めちゃくちゃ骨があって難しかったです。