JOI春合宿 2010-day4 highway

問題文 : 高速道路

解法 :
次のように, 2つの木を考える.

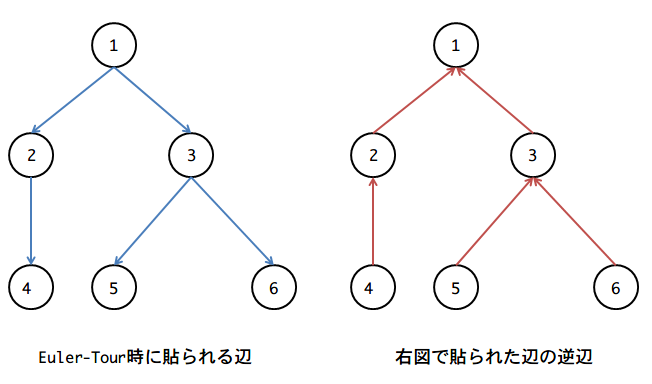
辺の更新のクエリが来た時は, euler-tourを行った時に、それぞれの辺が上りだったか、下りだったかを覚えておき処理する.

頂点uからvへ行くクエリが来た際は, u->lca(u, v)に行くときは逆辺の木, lca(u, v)->vに行くときはeuler-tourの木を使ってコストを求める.

例として, 上図の場合, 6->4へ行く時のコストは, 次のように辺をたどると良い.

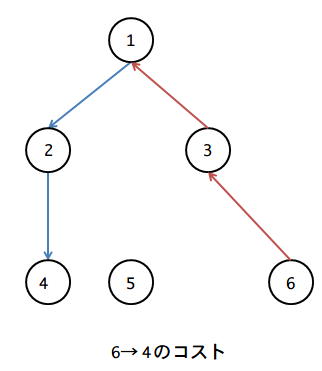
ローカル環境で試した際, スタックオーバーフローが起きたので, こちらの記事を参照した. (本番時と同じようにスタックサイズを設定してACを確認した.)

コード :

#include <cstdio>
#include <vector>
#include <algorithm>

#define MAX_N (100000)
#define UP (0)
#define DOWN (1)

using namespace std;

typedef pair<int, int> P;

struct Edge {
	int id, to;
	Edge(int id, int to) : id(id), to(to) {}
	Edge(){}
};

vector<Edge> G[MAX_N];

int size;
int costUp[MAX_N - 1], costDown[MAX_N - 1];
int bitUp[2 * MAX_N], bitDown[2 * MAX_N];
int es[2 * (MAX_N - 1)], esDir[MAX_N - 1];
int vs[2 * MAX_N - 1];
int depth[2 * MAX_N - 1];
int id[MAX_N];
P seg[1 << 19];

void add(int *bit, int pos, int val)
{
	while (pos <= 2 * MAX_N - 1){
		bit[pos] += val;
		pos += pos & -pos;
	}
}

int sum(int *bit, int pos)
{
	int ret = 0;
	
	while (pos){
		ret += bit[pos];
		pos &= (pos - 1);
	}
	
	return (ret);
}

void makeTree(int v, int prev, int d, int &k)
{
	vs[k] = v;
	id[v] = k;
	depth[k++] = d;
	
	for (int i = 0; i < G[v].size(); i++){
		Edge e = G[v][i];
		if (e.to != prev){
			esDir[e.id] = (v > e.to ? DOWN : UP);
			es[e.id * 2] = k;
			add(bitUp, k, 1); add(bitDown, k, 1);
			
			makeTree(e.to, v, d + 1, k);
			
			vs[k] = v;
			depth[k++] = d;
			es[e.id * 2 + 1] = k;
			add(bitUp, k, -1); add(bitDown, k, -1);
		}
	}
}


void initRMQ(int n)
{
	size = 1;
	while (size < n) size *= 2;
	for (int i = 0; i < 2 * size - 1; i++){
		seg[i].first = 999999; seg[i].second = -1;
	}
	
	for (int i = 0; i < n; i++){
		int k = i + size - 1;
		seg[k].first = depth[i]; seg[k].second = i;
		while (k){
			k = (k - 1) / 2;
			seg[k] = min(seg[k * 2 + 1], seg[k * 2 + 2]);
		}
	}
}

void init(int n)
{
	int k = 0;
	makeTree(0, -1, 0, k);
	
	initRMQ(2 * n - 1);
}

P getMin(int a, int b, int k = 0, int l = 0, int r = size)
{
	if (b <= l || r <= a){
		return (P(999999, -1));
	}
	
	if (a <= l && r <= b){
		return (seg[k]);
	}
	
	P left = getMin(a, b, k * 2 + 1, l, (l + r) / 2);
	P right = getMin(a, b, k * 2 + 2, (l + r) / 2, r);
	
	return (min(left, right));
}

int getLCA(int u, int v)
{
	int idu = id[u], idv = id[v];
	if (idu > idv) swap(idu, idv);
	
	return (vs[getMin(idu, idv + 1).second]);
}

int main()
{
	int n, m;
	
	scanf("%d %d", &n, &m);
	
	for (int i = 0; i < n - 1; i++){
		int a, b;
		scanf("%d %d", &a, &b);
		a--; b--;
		G[a].push_back(Edge(i, b));
		G[b].push_back(Edge(i, a));
		costUp[i] = costDown[i] = 1;
	}
	init(n);
	
	for (int i = 0; i < m; i++){
		char query[8];
		
		scanf("%s", query);
		
		if (query[0] == 'Q'){
			int from, to;
			scanf("%d %d", &from, &to);
			from--; to--;
			
			int p = getLCA(from, to);
			
			int cost = sum(bitUp, id[from]) - sum(bitUp, id[p]) + sum(bitDown, id[to]) - sum(bitDown, id[p]);
			
			printf("%d\n", cost);
		}
		else {
			int r, s, t;
			scanf("%d %d %d", &r, &s, &t);
			r--;
			
			if (esDir[r] == UP){
				add(bitDown, es[r * 2], s - costUp[r]);
				add(bitDown, es[r * 2 + 1], costUp[r] - s);
				add(bitUp, es[r * 2], t - costDown[r]);
				add(bitUp, es[r * 2 + 1], costDown[r] - t);
			}
			else {
				add(bitUp, es[r * 2], s - costUp[r]);
				add(bitUp, es[r * 2 + 1], costUp[r] - s);
				add(bitDown, es[r * 2], t - costDown[r]);
				add(bitDown, es[r * 2 + 1], costDown[r] - t);
			}
			costUp[r] = s; costDown[r] = t;
		}
	}
	
	return (0);
}