JOI Open Contest 2015 - Sterilizing Spray

しばらく競プロをやっていなかったのと、ちょっと卒論の気晴らしをしたかったので、昔解いていなかった問題を漁ってました。
結果恐ろしいくらい時間を溶かしました……今から進捗出します。ごめんなさい(´；ω；｀)

ジャッジもテストデータも今は無いので、サンプルを通した程度で解けたものと判断しています。
愚直解とあとで出力を比較してみます。

問題概要

$N$ 要素からなる配列 $C$ と、整数 $K$ が与えられる。次の 3 つのタイプのクエリを合計 $Q$ 個処理せよ。

$a_i$ 番目の要素の値を $b_i$ に書き換える。
$l_i$ 番目の要素から $r_i$ 番目の要素を $K$ で割る。小数点以下は切り捨てる。
$l_i$ 番目の要素から $r_i$ 番目の要素までの和を求める。

$1 \leqq N, Q \leqq 10^5$
$1 \leqq K \leqq 10$
$1 \leqq C_i, b_i \leqq 10^9$

解法

まず、 $K = 1$ のときのことを考えると、2 番目のクエリは配列に影響を及ぼさない。
このとき、問題は一点更新区間和の問題に落ちるため BIT で解くことが出来る。

$K > 1$ のとき、一点更新と区間和のクエリはセグメント木で高速に処理することが可能である。
しかし、区間の除算をうまく扱うのが難しい。
そこで、配列の要素を次の図のように $K$ 進数として表現することを考えてみる。

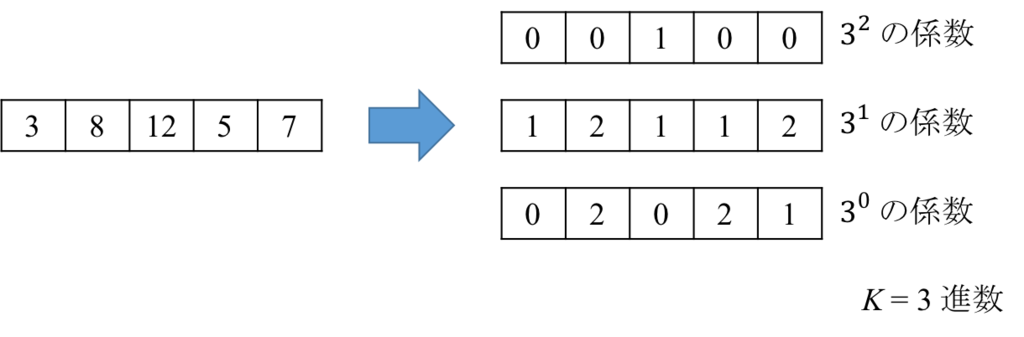
すると、区間の除算は、次の図のように、 $K$ 進数表示の各基数の係数をシフトすることに対応することが分かる。

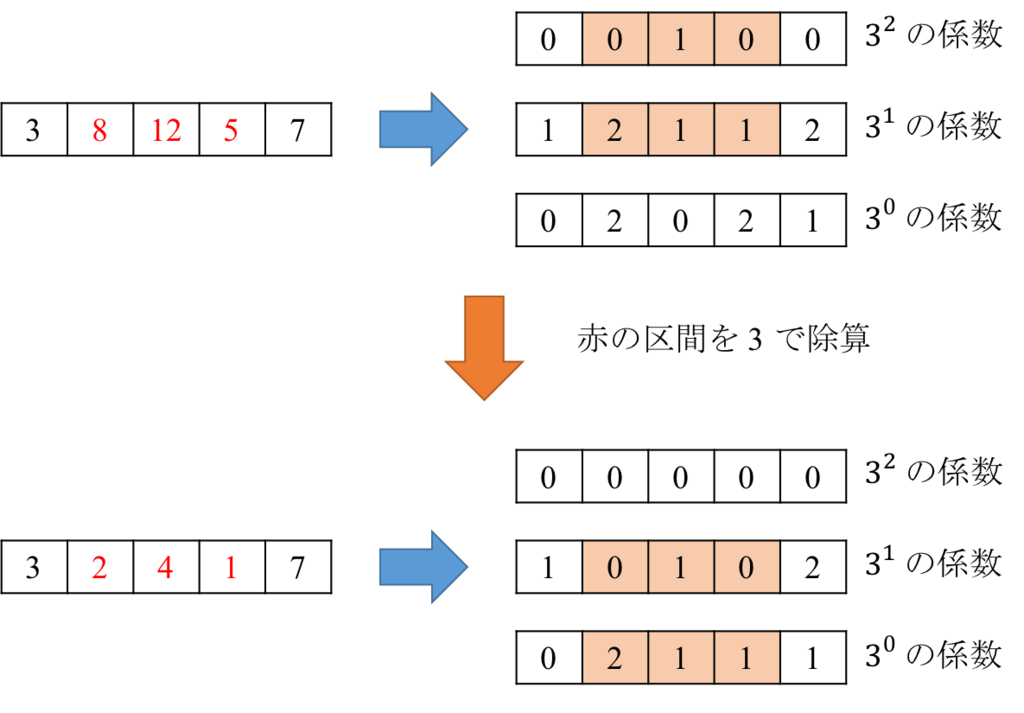
これは、セグメント木を $\log_{K} 10^9$ 用意し、部分木をまるごと入れ替えることで対応できる。
入れ替える部分木はたかだか $O(\log N)$ 本で抑えられるので、 $M = \log_{K} 10^9$ として $O(M \log N)$ 時間で除算クエリに対応できる。

セグメント木の機能としては、

区間 $l,\ r$ の数値を全て $0$ に書き換える。
一点 $x$ の数値を $a$ に書き換える。
区間 $l,\ r$ の和を求める。

というものが実装できれば、全ての基数についての和を求めれば全てのクエリに答えることが出来る。
全体の計算量は $O(QM \log N)$ 時間となる。

色々と手を抜いて実装したので、手元の環境だと 6 秒近くかかりました……
部分木の入れ替えの実装で混乱してしまいました。~~こんなことしなくても解けそう~~。

コード :

#include <bits/stdc++.h>

#define MAX_N (100010)
#define MAX_Q (100010)
#define MAX_S (131072)

using namespace std;

typedef long long Int;

class BIT {
	Int A[MAX_N + 1];
public:
	BIT(){
		memset(A, 0, sizeof(A));
	}
	void add(int p, Int x){
		for (p++; p <= MAX_N; p += p & -p) A[p] += x;
	}
	Int sum(int p){
		Int ret = 0;
		for (p++; p; p &= (p - 1)) ret += A[p];
		return (ret);
	}
};

struct Node {
	Int val;
	bool id;
	bool reset;
	Node *ch[2];
};

Node seg[30][2 * MAX_S - 1];

int pos, idx = 0;
Node *parents[30][32], *children[30][32];

inline void evaluate(Node *p)
{
	if (p->reset){
		p->val = 0;
		if (p->ch[0] != nullptr) p->ch[0]->reset = true;
		if (p->ch[1] != nullptr) p->ch[1]->reset = true;
	}
	p->reset = false;
}

inline void updateNode(Node *p)
{
	p->val = p->ch[0]->val + p->ch[1]->val;
}

void update(Node *p, int a, int b, int x, int l = 0, int r = MAX_S)
{
	evaluate(p);
	if (b <= l || r <= a) return;
	if (a <= l && r <= b){
		p->val = x;
		return;
	}
	update(p->ch[0], a, b, x, l, (l + r) / 2);
	update(p->ch[1], a, b, x, (l + r) / 2, r);
	updateNode(p);
}

void getInterval(Node *p, Node *pp, int a, int b, int l = 0, int r = MAX_S)
{
	if (b <= l || r <= a) return;
	if (a <= l && r <= b){
		parents[pos][idx] = pp;
		children[pos][idx++] = p;
		return;
	}
	getInterval(p->ch[0], p, a, b, l, (l + r) / 2);
	getInterval(p->ch[1], p, a, b, (l + r) / 2, r);
}

void modify(Node *p, int a, int b, int l = 0, int r = MAX_S)
{
	evaluate(p);
	if (b <= l || r <= a) return;
	if (a <= l && r <= b) return;
	modify(p->ch[0], a, b, l, (l + r) / 2);
	modify(p->ch[1], a, b, (l + r) / 2, r);
	updateNode(p);
}

void clear(Node *p, int a, int b, int l = 0, int r = MAX_S)
{
	evaluate(p);
	if (b <= l || r <= a) return;
	if (a <= l && r <= b){
		p->reset = true;
		evaluate(p);
		return;
	}
	clear(p->ch[0], a, b, l, (l + r) / 2);
	clear(p->ch[1], a, b, (l + r) / 2, r);
	updateNode(p);
}

Int getSum(Node *p, int a, int b, int l = 0, int r = MAX_S)
{
	evaluate(p);
	if (b <= l || r <= a) return (0);
	if (a <= l && r <= b) return (p->val);
	Int lsum = getSum(p->ch[0], a, b, l, (l + r) / 2);
	Int rsum = getSum(p->ch[1], a, b, (l + r) / 2, r);
	updateNode(p);
	return (lsum + rsum);
}

int C[MAX_N];
int S[MAX_Q], T[MAX_Q], U[MAX_Q];

int main()
{
	int N, Q, K;

	scanf("%d %d %d", &N, &Q, &K);

	for (int i = 0; i < N; i++){
		scanf("%d", C + i);
	}

	for (int i = 0; i < Q; i++){
		scanf("%d %d %d", S + i, T + i, U + i);
	}

	if (K == 1){
		BIT bit;
		for (int i = 0; i < N; i++) bit.add(i, C[i]);
		for (int i = 0; i < Q; i++){
			if (S[i] == 1){
				bit.add(T[i] - 1, (Int)U[i] - C[T[i] - 1]);
				C[T[i] - 1] = U[i];
			}
			else if (S[i] == 3){
				printf("%lld\n", bit.sum(U[i] - 1) - bit.sum(T[i] - 2));
			}
		}
		return (0);
	}

	for (int i = 0; i < 30; i++){
		for (int j = 0; j < 2 * MAX_S - 1; j++){
			if (j < MAX_S - 1){
				seg[i][j].ch[0] = &seg[i][j * 2 + 1];
				seg[i][j].ch[1] = &seg[i][j * 2 + 2];
			}
			else {
				seg[i][j].ch[0] = nullptr;
				seg[i][j].ch[1] = nullptr;
			}

			seg[i][j].id = (j + 1) % 2;
			seg[i][j].reset = false;
			seg[i][j].val = 0;
		}
	}

	for (int i = 0; i < N; i++){
		Int v = C[i];
		for (int j = 0; j < 30; j++){
			Int s = v % K;
			update(&seg[j][0], i, i + 1, s);
			v /= K;
		}
	}

	int ct = 0;
	for (int i = 0; i < Q; i++){
		if (S[i] == 1){
			Int v = U[i];
			for (int j = 0; j < 30; j++){
				Int s = v % K;
				update(&seg[j][0], T[i] - 1, T[i], s);
				v /= K;
			}
		}
		if (S[i] == 2){
			for (int j = 0; j < 30; j++){
				modify(&seg[j][0], T[i] - 1, U[i]);
			}

			clear(&seg[0][0], T[i] - 1, U[i]);

			for (int j = 0; j < 30; j++){
				pos = j;
				idx = 0;
				getInterval(&seg[j][0], nullptr, T[i] - 1, U[i]);
			}

			for (int j = 0; j < idx; j++){
				int id = children[0][j]->id;
				for (int k = 0; k < 30; k++){
					parents[k][j]->ch[id] = children[(k + 1) % 30][j];
				}
			}
			for (int j = 0; j < 30; j++){
				modify(&seg[j][0], T[i] - 1, U[i]);
			}
			ct++;
		}
		if (S[i] == 3){
			Int pK = 1;
			Int ans = 0;
			for (int j = 0; j < 30; j++){
				ans += pK * getSum(&seg[j][0], T[i] - 1, U[i]);
				pK *= K;
			}
			printf("%lld\n", ans);
		}
	}

	return (0);
}

Lilliput Steps

小さな一歩から着実に. 数学やプログラミングのことを書きます.

JOI Open Contest 2015 - Sterilizing Spray

問題概要

解法